Chapitre 14 Analyse Sémantique Latente (ASL/LSA)
L’analyse sémantique latente s’est développée sous le travail des linguistiques, et la généralisation d’outils tels que les moteurs de recherche. (???)

Le retour sur histoire que nous fait l’auteur, ainsi que sa description des différents principes de calculs et vigilances pour l’analyste à garder en mémoire, renseigne sur les heuristiques de cette méthode : Son principe fondateur est de réussir à retrouver dans une collection de documents, un ensemble de patterns présents ou absents, dans un système d’équations s’exprimant chacune en fonction des autres. Cette expression réciproque s’opère à l’aide de la décomposittion spectrale de chacun de ces mots. En ce sens, elle peut se comprendre comme un résultat de la recherche allant dans la quantisation des vecteurs, la régression multinomiale, ou bien encore la topologie, comme identifiée par Fodor en 2002 (???) ou d’autres applications croisées. (???)
Nous supprimons les lemmes propres au entitées nommées étudiées.
Pour les détails et l’implémentations du code, se réferrer à C. Benavent.
annot_udd <- df_trt_annot%>%filter(Marque=="Cobol")
dfm_lsa <- dfm(annot_udd$lemma,
tolower = TRUE,
what = "word")
mylsa <- textmodel_lsa(dfm_lsa,2)
proxD<-mylsa$docs[, 1:2]
#rtsne
tsne_out <- Rtsne(proxD, dims = 2, initial_dims = 100,
perplexity = 20, theta = 0.5, check_duplicates = FALSE,
pca = TRUE, max_iter = 300)
x<-tsne_out$Y
x<-as.data.frame(x)
x$Facteur_1<-x[,1]
x$Facteur_2<-x[,2]
x<-cbind(annot_udd,x)
df<-subset(x)
prox<-mylsa$features[, 1:2]
terms<-as.data.frame(prox)
#rtsne
tsne_out <- Rtsne(terms, dims = 2, initial_dims = 50,
perplexity = 20, theta = 0.5, check_duplicates = FALSE,
pca = TRUE, max_iter = 300)
x<-tsne_out$Y
terms$term<-row.names(prox)
plot<-cbind(x,terms)
plot$Facteur_1<-plot[,1]
plot$Facteur_2<-plot[,2]
ggplot(plot,aes(x = Facteur_1,y=Facteur_2))+geom_point()+geom_text(aes(label=term),hjust=0.5, vjust=0.5, size=2.5)+ ggtitle("Analyse sémantique autour du Langage Cobol")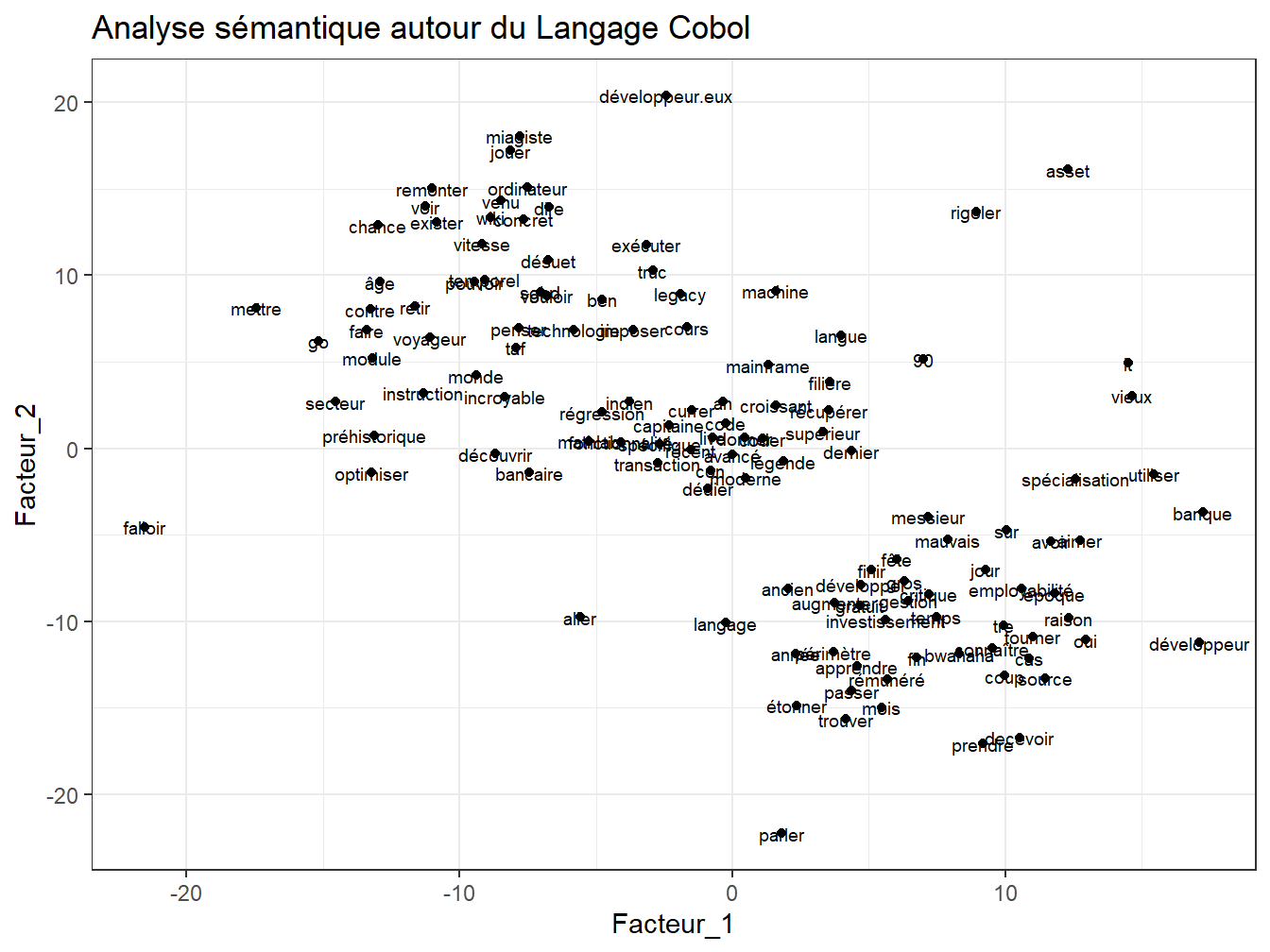
Figure 14.1: Analyse de sémantique Latente sur Cobol
Aucun filtrage sur la dfm n’est appliquée sur les mots associés à Cobol. Leur effectif est bien plus réduit que celui des mots de javascript, où l’on applique un filtrage afin de ne tenir compte que des termes supérieurs à 9.
###
annot_udd <- df_trt_annot%>%filter(Marque=="javascript")
dfm_lsa <- dfm(annot_udd$lemma,
tolower = TRUE,
what = "word",
docvars = "Marque")
dfm_lsa <-
dfm_trim(
dfm_lsa,
min_termfreq = 10)
mylsa <- textmodel_lsa(dfm_lsa,2)
proxD<-mylsa$docs[, 1:2]
#rtsne
tsne_out <- Rtsne(proxD, dims = 2, initial_dims = 100,
perplexity = 20, theta = 0.5, check_duplicates = FALSE,
pca = TRUE, max_iter = 300)
x<-tsne_out$Y
x<-as.data.frame(x)
x$Facteur_1<-x[,1]
x$Facteur_2<-x[,2]
x<-cbind(annot_udd,x)
prox<-mylsa$features[, 1:2]
terms<-as.data.frame(prox)
#rtsne
tsne_out <- Rtsne(terms, dims = 2, initial_dims = 50,
perplexity = 20, theta = 0.5, check_duplicates = FALSE,
pca = TRUE, max_iter = 300)
x<-tsne_out$Y
terms$term<-row.names(prox)
plot<-cbind(x,terms)
plot$Facteur_1<-plot[,1]
plot$Facteur_2<-plot[,2]
ggplot(plot,aes(x = Facteur_1,y=Facteur_2))+geom_point()+geom_text(aes(label=term),hjust=0.5, vjust=0.5, size=2.5)+ ggtitle("Analyse sémantique autour du Langage javascript")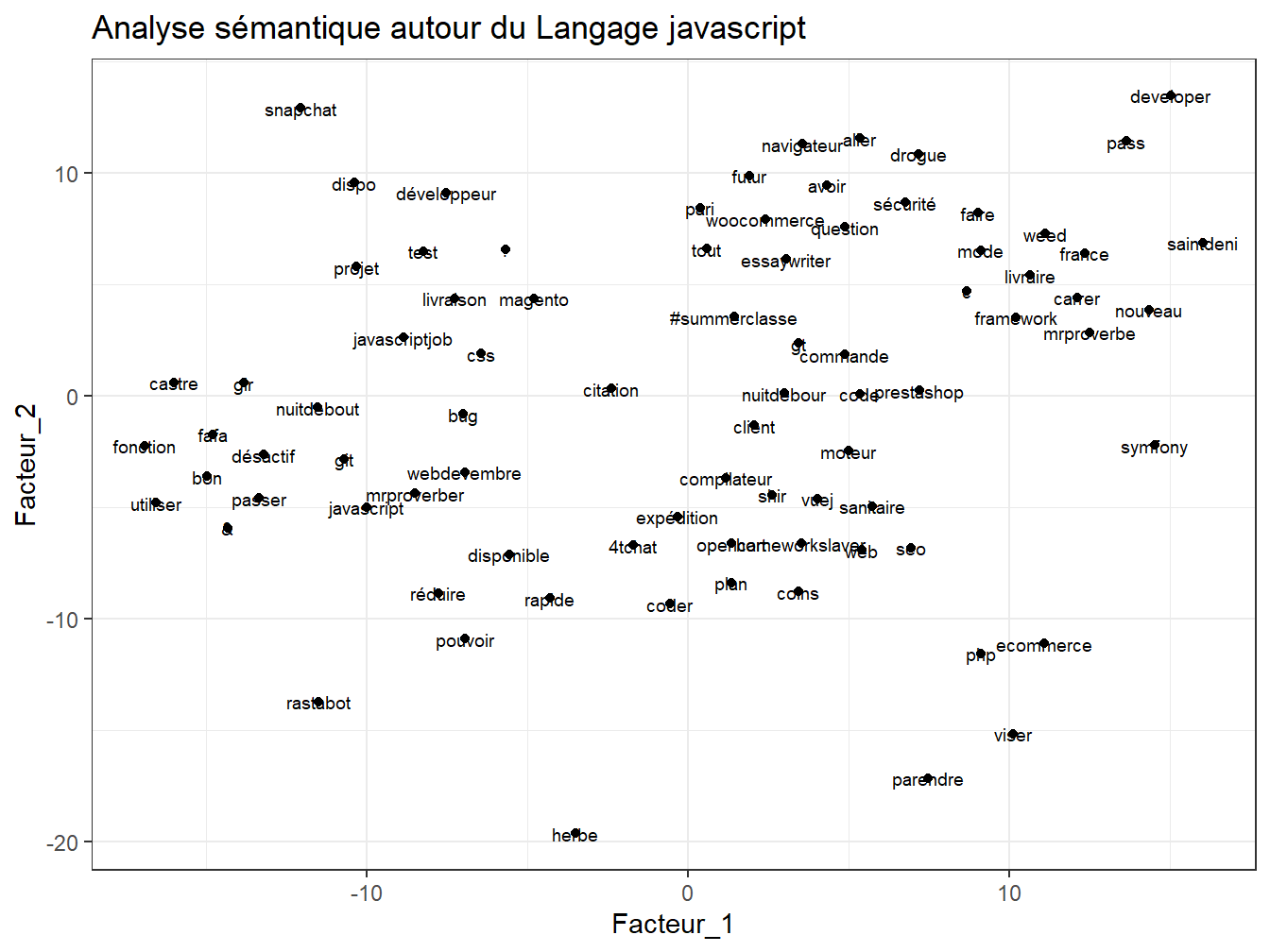
Figure 14.2: Analyse de sémantique Latente sur javascript
Les différentes visualisations produites montrent que les langages baignent, outre certains phénomènes de pollution, dans un vocabulaire emprunt à leurs domaines technico-fonctionnels propres. On observe la présence des domaines du Web en ce qui concerne “JS” et de la gestion financière des grands groupes pour ce qui concerne le vieil ami Cobol.
En outre, les mots associés à ce dernier sont dans une thématique métier plus professionnelle, tant d’un point de vue de l’ingénierie informatique que financière. L’utilisation de javascript semble plus orientée vers son environnement informatique digital, web et outils propres (frameworks et apparentés) plus qu’au domaine fonctionnel sur lesquels il est potentiellement appliqué.
Cela peut également expliquer en partie les différentes populations pressenties : évoquer “Cobol” nécessite de s’intéresser à l’informatique, ce langage est inconnu pour bon nombre d’informaticiens débutants et invisible du grand public, en revanche, plein de tutoriels et de parcours de formations proposent des travaux pratiques, qui permettent aux apprennants de développer un robot à l’architecture plus ou moins complexe, dont la durée de vie se limite pour les plus élémentaires qu’à un script javascript.
Cependant, difféfentes variantes du modèle classique de LSA, plus ou moins probabilistes ou supervisées existent, et leurs spécificités permet de comprendre les équivalences et traits communs entre les divers algortihmes retenus ici pour l’étude. (???)(???)
14.0.1 Non-negative Matrix Factorization
Le fonctionnement de cet algorithme de factorisation est de décomposer le fichier d’entrée \(A\) en deux matrices, \(W\), tel que \(W= u\) x \(k\) et H, tel que \(H = k\) x \(v\) ou \(k\) est ici déterminé à l’aide d’une fonction intégrée au package R [NMF], et déterminé selon le corpus fourni à \(k = 15\) dimensions. Lorsque cet algorithme opère une coefficientisation par approximation de la décomposition du fichier \(A\), en deux fichiers \(W\) & \(H\) de rang \(k\), il nous permet de réaliser le produit matriciel de ces deux fichiers de sorties, et donc de proposer une réorganisation du fichier \(A\) selon \(k\) facteurs sous-jacents, et d’ainsi obtenir le rang de factorisation non-négative. De manière naturelle, il serait intéressant de savoir si l’on peut observer un modèle théorique de vocabulaires spécifiques dans la réorganisation finale obtenue.Ici donc, la matrice d’entrée A est composée des 4 langages précités, et de 3641 mots retenus pour l’étude, composés des verbes, noms et adjectifs.
mydfm_k <- dfm(df_trt_annot$lemma,
tolower = TRUE,
what = "word",
groups = df_trt_annot$Marque)
mydfm.un.trim <-
dfm_trim(
mydfm_k,
min_termfreq = 20)
df_txt <- mydfm.un.trim %>%
convert(to = "matrix",docid_field=TRUE)
#detach("package:NMF", unload = TRUE)
my.nmf <- nmf(df_txt,15,nrun=30,.opt="vp3",seed = 1253)##
Runs: |
Runs: | | 0%
Runs: |
Runs: |==================================================| 100%
## System time:
## user system elapsed
## 7.83 0.02 12.06#plot(my.nmf)
w <- my.nmf@fit@W
h <- my.nmf@fit@H
res <- as.data.frame(w%*%h)
#res$Marque <- rownames(res)
t_ <- as.data.frame(t(res))
t_ <- t_[1:nrow(t_),]
tcob<-t_%>%select(Cobol)
tcob <- tcob%>%arrange(desc(Cobol))%>%head(50)
tcob$Cobol <- rownames(tcob)
tjas<-t_%>%select(javascript)
tjas <- tjas%>%arrange(desc(javascript))%>%head(50)
tcob$javascript <- rownames(tjas)
rownames(tcob) <- NULLAfin de visualiser les résultats produits, nous utilisons des fonctions de type heatmap, adaptées à la représentations de matrices.
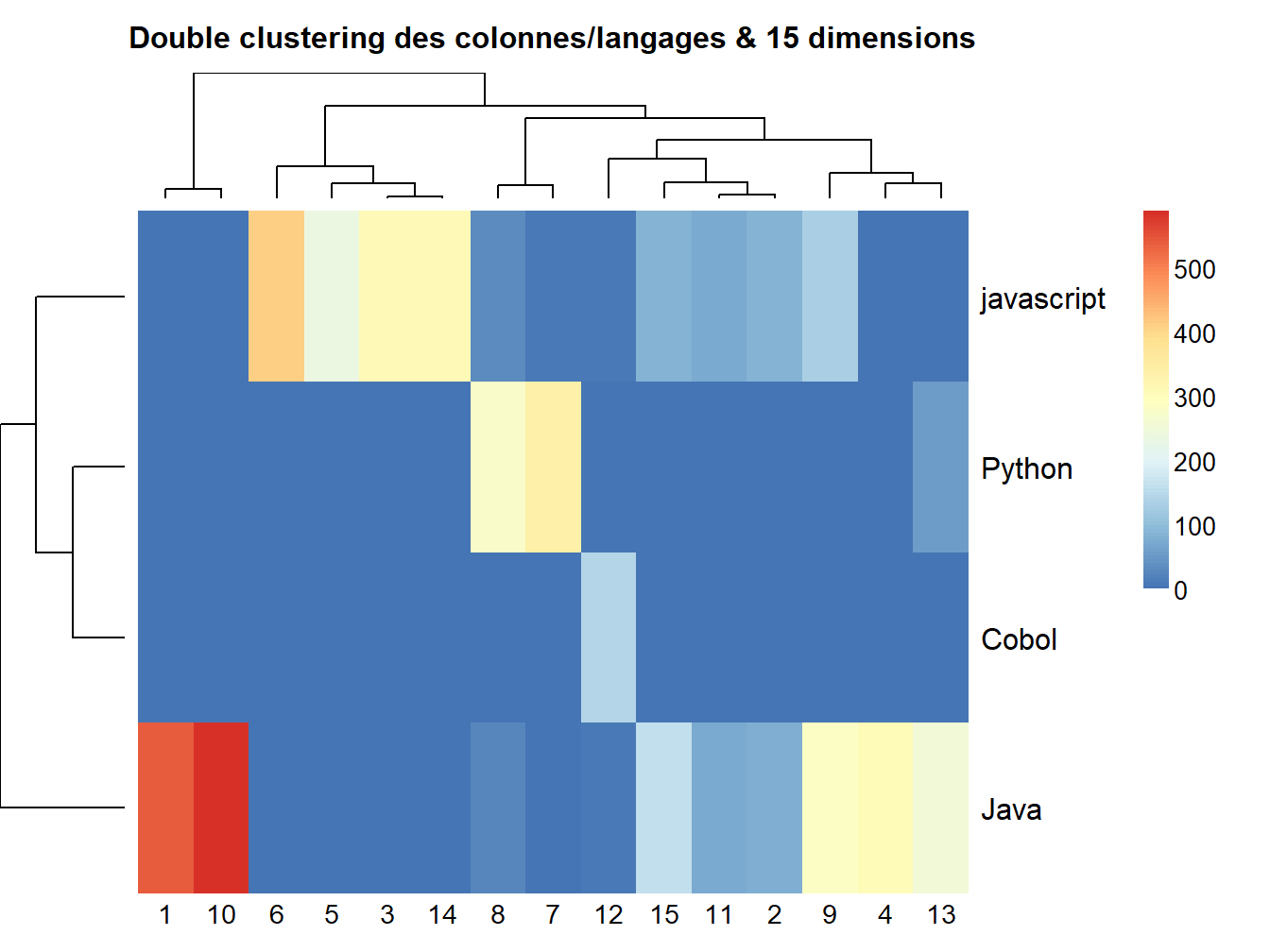
Figure 14.3: Double clustering des colonnes/langages & 15 dimensions
La probabilité qu’un langage appartienne aux dimensions, suivie de la probabilité qu’un mot appartienne aux dimensions.
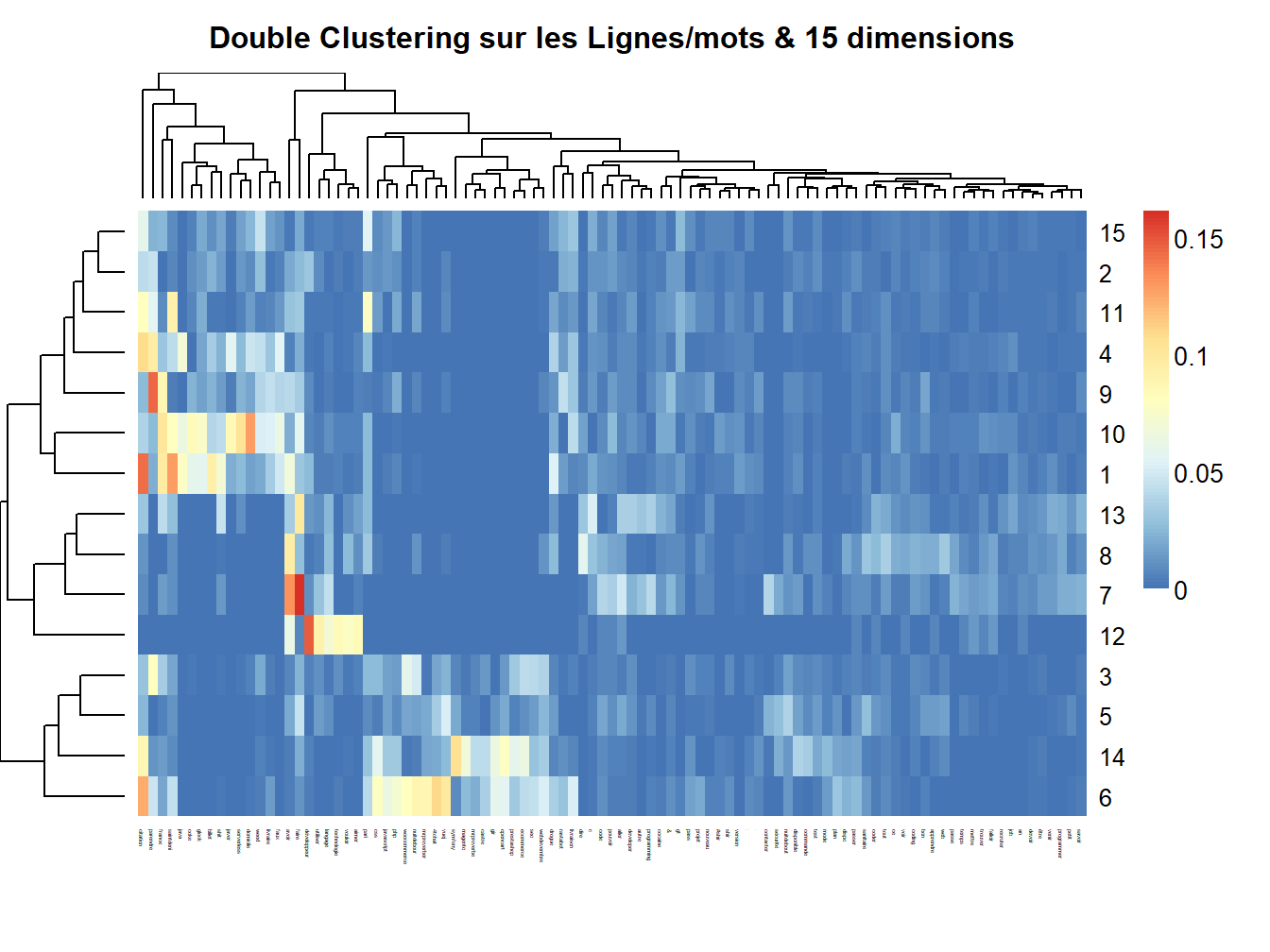
Figure 14.4: Double Clustering sur les Lignes/mots & 15 dimensions
Les représentations graphiques des matrices \(W\) et \(H\) permettent d’observer la distributivité des mots selon les facteurs (\(H\)) ou les variables (\(W\)), le gradient de coloration étant proportionnel à la covariance des éléments. (???)
En réalisant le produit matriciel de ces deux tableaux il est possible, d’obtenir la liste des mots les plus typiques de la modalité de variable étudiée, ici le langage de programmation.
Les matrices de coefficients représentent des résultats intermédiaires, permettant de cenraliser dans un tableau de données l’ensemble des expressions linéaires possibles d’un système en fonction de ses paramètres et positions. Le consensus, s’obtient suites aux différentes itérations demandées, ici fixées à 30.
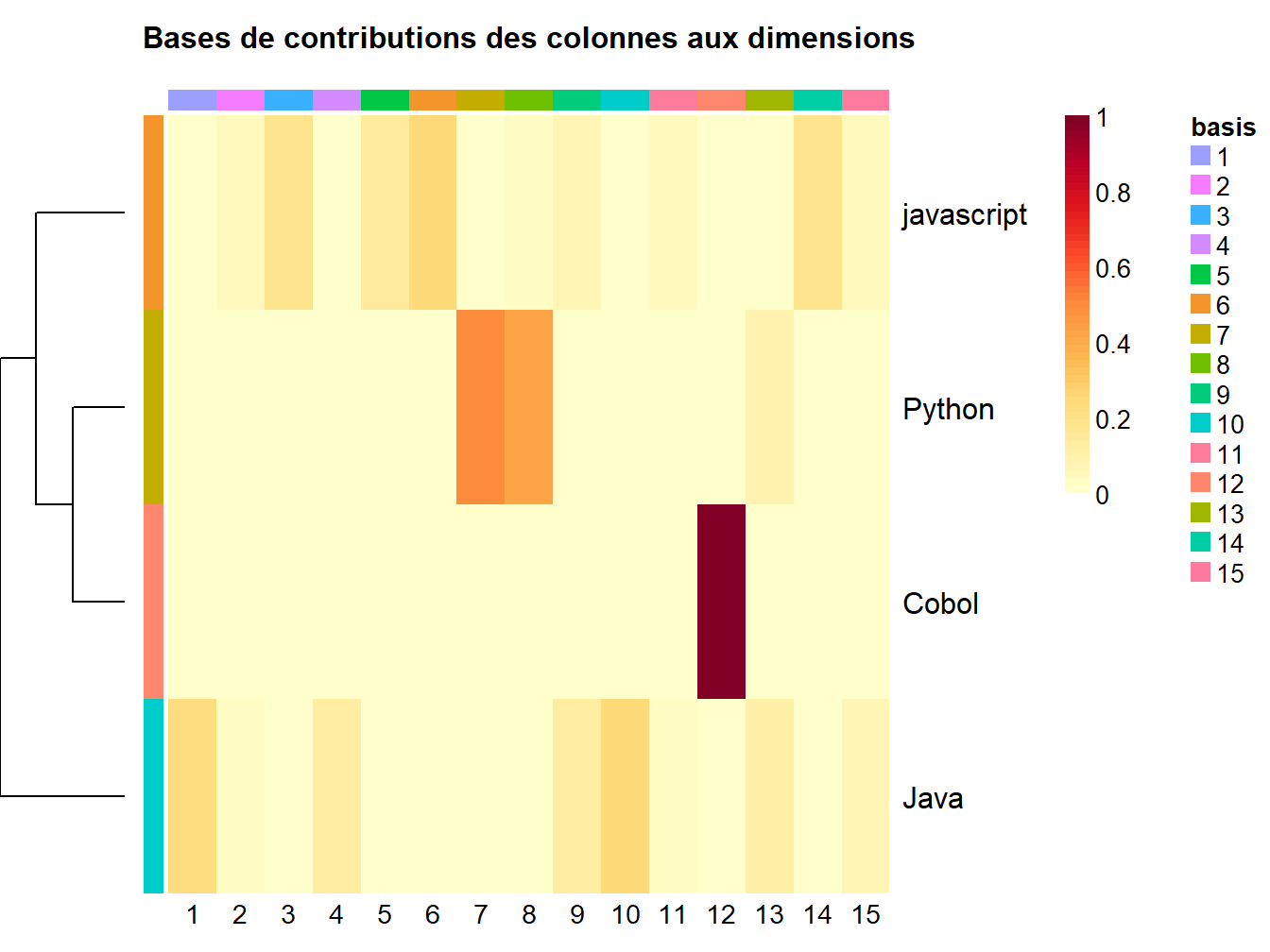
Figure 14.5: Contributions des colonnes aux dimensions
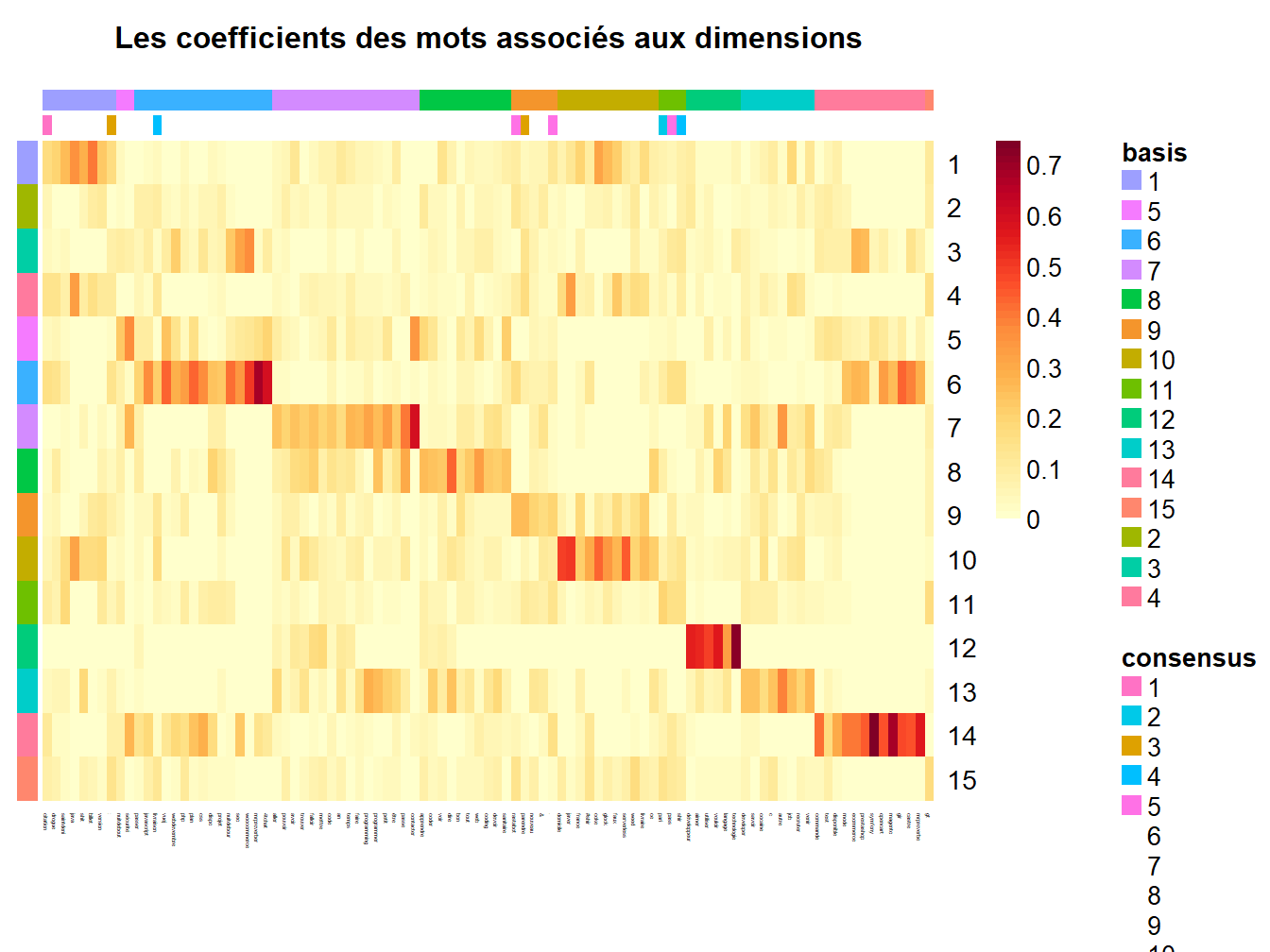
Figure 14.6: Coefficients des associations des mots aux dimensions
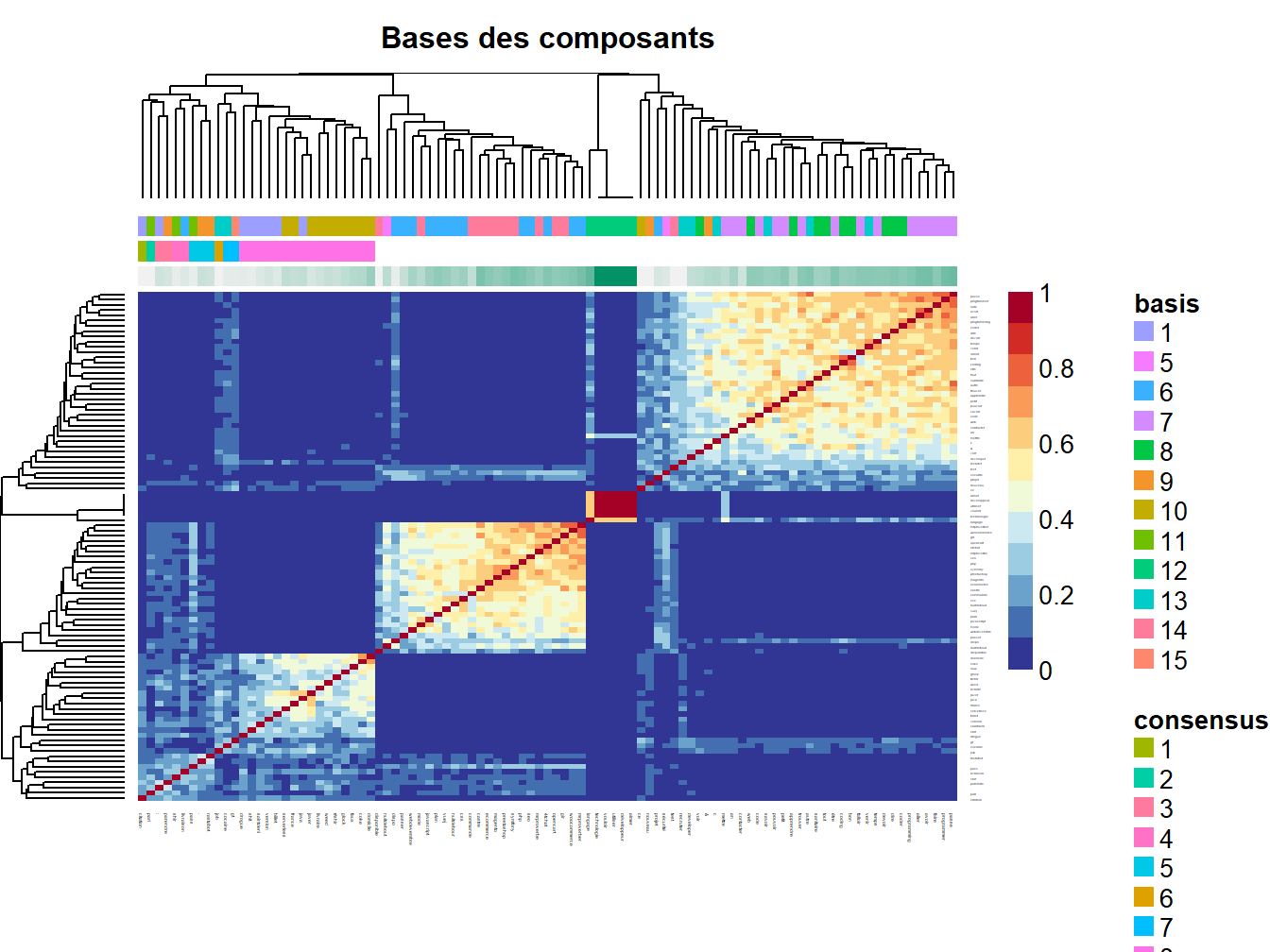
Figure 14.7: Map de consensus entre les 30 itérations
14.1 Conclusion
La branche mathématique appliquée au calcul matriciel développe depuis longtemps un important travail de recherche sur les propriétés mathématiques de cet objet, (???) dont les problèmes se classifient selon une échelle de difficulté NP. (???) Plusieurs questions ont été abordées, notamment sur l’interprétabilité des facteurs (???), l’ajustement de certains paramètres comme la co-entropie, (???) la détection du nombre de composantes, (???) ou encore la divergence B. (???) Un important travail de recherche faisant l’objet d’une thèse en 2014 documente historiquement et techniquement les diverses approches de factorisation matricielle et plus précisément, celles appliquées aux matrices de données non-négatives dont l’hypothèse méthodologique de calculs admettent “la positivité des composantes” ou se basent sur leur “non-négativité”. (???) Aujourd’hui, la généralisation de son utilisation est possible pour les utilisateurs de différents langages de programmation,(???) et plusieurs travaux témoignent de ses applications courantes à divers secteurs : l’analyse d’image, le text mining, (???) l’analyse spectrophotométrique, (???) ou bien encore l’analyse financière,(???) et la détection des fake news. (???)
Ces techniques se sont développées en se confrontant aux différentes structures de données et développements des courants de recherche en mathématiques. Leur existence n’empêche pas leur utilisation conjointe à des fins de classifications, ou réduction de dimensions. (???)
Part ailleurs, d’autres modèles existent et permettre de comprendre les différentes équivalences entre les méthodes décrites ci-dessus. (???) En ce sens, le travail de Pochon en 2020 dresse un panorama plus situé, des différentes techniques et de leurs enjeux, tant en termes d’accessibilité, que d’applicabilité. (???)